자바스크립트로 구현한 선택정렬 알고리즘 (Selection sort in Javascript)

남양주개발자

2020. 11. 19. 07:20

728x90

자바스크립트로 구현한 선택정렬 알고리즘 (Selection sort in Javascript)

선택정렬 알고리즘은 정렬 알고리즘을 공부하다보면 버블정렬만큼 익숙하게 들어본 정렬 알고리즘 중 하나일 것입니다. 버블정렬 만큼 구현하기 쉽고, 기업 코딩테스트를 하다보면 한번씩 문제로 나오곤 하는 선택정렬 알고리즘!

이번 포스팅에서는 선택정렬 알고리즘의 특징과 구현 예시에 대해서 소개하도록 하겠습니다.

선택 정렬이란?

선택정렬 알고리즘의 컨셉은 요소들이 들어갈 위치는 이미 정해져있다는 것에 있습니다. 예를 들어, 배열의 첫 번째 자리에는 배열 요소들 중 가장 작은 요소가 들어가면 되겠죠? 그리고 두 번째 자리에는 그 다음 가장 작은 요소를 선택해서 그 자리에 넣으면 됩니다. 이렇게 배열이 끝날 때까지 이 단계를 진행하면 됩니다.

선택정렬 알고리즘 예시

선택정렬 알고리즘을 좀 더 쉽게 이해하기 위해 코드를 보기 전에 해당 자료를 한번 보시면 좀 더 이해가 쉬울 수 있습니다.

선택정렬 알고리즘에 대한 동영상 예시

정렬과정

배열 중에 최솟값이 위치한 index를 찾습니다.
최솟값이 위치한 index의 값과 맨 처음의 index 값을 swap합니다.
맨 처음의 index를 제외한 나머지 배열에 대해서 1,2 단계를 진행합니다.
하나의 요소가 남을 때까지 위 1~3 과정을 반복합니다.

배열의 초기 값이 [9,2,5,1,3]로 저장되어 있다고 가정하고 배열의 순서를 오름차순으로 정렬해보도록 하겠습니다.

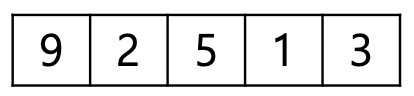
// 정렬 전 : [9,2,5,1,3]

// 1회전
[9,2,5,1,3]
// 최솟값을 탐색한다. 최솟값의 인덱스는 3, 첫 번째 값과 최솟값의 인덱스의 값을 swap한다.
결과: [1,2,5,9,3]

// 2회전
[1,2,5,9,3]
// 최솟값을 탐색한다. 최솟값의 인덱스는 1, 시작 값과 최솟값의 인덱스 값은 같음으로 유지한다.
결과: [1,2,5,9,3]

// 3회전
[1,2,5,9,3]
// 최솟값을 탐색한다. 최솟값의 인덱스는 4, 시작 값과 최솟값의 인덱스의 값을 swap한다.
결과: [1,2,3,9,5]

// 4회전
[1,2,3,9,5]
// 최솟값을 탐색한다. 최솟값의 인덱스는 4, 시작 값과 최솟값의 인덱스의 값을 swap한다.
결과: [1,2,3,5,9]

// 최종 정렬 결과 : [1,2,3,5,9]

1회전

첫 번째 요소의 인덱스를 minIndex(0)로 지정한 후, 두 번째 요소(2)부터 마지막 요소(3)까지 비교하여 가장 작은 값을 가진 인덱스의 값을 첫 번째 요소와 교환합니다. 이 과정에서 요소를 총 4번 비교합니다. minIndex는 3이므로 minIndex 값인 1과 첫 번째 요소의 값 9를 교환합니다.

2회전

첫 번째 요소는 정렬이 완료되었으므로 두 번째 요소부터 순회를 시작합니다. 두 번째 요소의 인덱스를 minIndex(1)로 지정한 후, 세 번째 요소(5)부터 마지막 요소(3)까지 비교하여 가장 작은 값을 가진 인덱스의 값을 두 번째 요소와 교환합니다. 이 과정에서 요소를 총 3번 비교합니다. 현재 index의 값과 minIndex 값이 같으므로 교환하지 않고 2회전을 종료합니다. (2회전의 최솟값이 현재 index의 값이기 때문에 swap할 필요가 없음)

3회전

두 번째 요소까지 정렬이 완료되었으므로 세 번째 요소부터 순회를 시작합니다. 세 번째 요소의 인덱스를 minIndex(2)로 지정한 후, 네 번째 요소부터(9) 마지막 요소(3)까지 비교하여 가장 작은 값을 가진 인덱스의 값을 세 번째 요소와 교환합니다. 이 과정에서 요소를 총 2번 비교합니다. minIndex는 4이므로 minIndex 값인 3과 세 번째 요소의 값 5를 교환합니다.

4회전

세 번째 요소까지 정렬이 완료되었으므로 네 번째 요소부터 순회를 시작합니다. 네 번째 요소의 인덱스를 minIndex(3)로 지정한 후, 마지막 요소(5)와 비교하여 교환합니다. 이 과정에서 요소를 총 1번 비교합니다. minIndex는 4이므로 네 번째 요소(9)와 마지막 요소(5)를 교환합니다.

선택정렬의 특징(장단점)

시간복잡도

선택정렬은 최선, 최악, 평균 모두 O(n2)의 시간복잡도를 가지고 있습니다. 선택정렬의 비교 횟수는 초기 minIndex를 설정해주는 외부 루프 (n-1)번 그리고 순회하면서 최솟값을 찾는 내부 루프(n-1, n-2, ..., 1)번으로 총 두 개의 반복문이 실행됩니다.

최선(Best)	평균(Avg)	최악(Worst)
O(n2)	O(n2)	O(n2)

장점

실제 사람들이 직접 정렬한다고 할 때 진행하는 방식과 가장 유사하다.
알고리즘 구현 난이도가 굉장히 낮고, 단순한 정렬 알고리즘이다.
제자리 정렬(In-place sort)의 특징을 가지고 있기 때문에, 주어진 공간 외에 추가적인 메모리를 필요로 하지 않는다. 메모리가 제한적인 상황에서 메모리를 추가적으로 할당해서 사용하는 상황에 한해서는 추가적인 메모리를 요하는 정렬 알고리즘에 비해 성능상의 이점이 있을 가능성이 있다.

단점

현재 값이 최솟값임에도 불구하고 최솟값을 찾기 위한 순회 과정을 진행한다. (불필요한 순회과정이 포함되어 있다.)
최솟값을 찾는 횟수가 정해져있다. (n - 1, n - 2, ..., 1)
O(n2)의 시간복잡도를 가진 만큼 퍼포먼스 측면에서 좋지 않다.
불안정 정렬(unstable sort)로써 동일한 값에 대해 기존의 순서가 뒤바뀔 수 있는 정렬 방식이다.

소스 코드

아래 소스 코드는 자바스크립트(Javascript) ES6 문법으로 구현한 예시입니다. 자바스크립트(Javascript) ES6 문법 중 구조 분해 할당 구문을 활용해서 요소 swap을 처리했습니다.

// 선택정렬 ES6
const selectionSort = (arr) => {
	for (let i = 0; i < arr.length - 1; i++) {
  	let minIndex = i;
    for (let j = i + 1; j < arr.length; j++) {
    	if (arr[minIndex] > arr[j]) {
				minIndex = j
      }
    }
    
    if (minIndex !== i) {
    	[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
    }    
  }
  
  return arr;
}

// 선택정렬
const selectionSort = (arr) => {
	for (let i = 0; i < arr.length - 1; i++) {
  	let minIndex = i;
    for (let j = i + 1; j < arr.length; j++) {
    	if (arr[minIndex] > arr[j]) {
				minIndex = j
      }
    }
    
    if (minIndex !== i) {
    	const temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }    
  }
  
  return arr;
}

이중 선택 정렬 (Double Selection Sort)

최소 최대 정렬이라고도 불리는 이중 선택 정렬은 선택정렬에서 최솟값을 찾는 과정에서 최댓값까지 함께 찾아 최솟값과 최댓값을 동시에 정렬한다면 정렬하는 시간이 반으로 줄지 않을까라는 아이디어로 등장한 정렬 알고리즘입니다. 이중 선택 정렬은 선택정렬이 순회하면서 최솟값을 찾는 과정에 최댓값까지 같이 찾은 다음 최솟값은 앞쪽에 최댓값은 뒤쪽에 배치하면서 정렬을 진행합니다. 이중 선택 정렬을 사용하면 일반 선택정렬보댜 반복횟수가 반정도 줄게 됩니다. (근데 console.time으로 요소 100,000개에 대한 알고리즘 수행시간을 체크해봤는데, 일반 선택정렬보다 이중 선택 정렬이 더 느리게 찍힌건 왜 때문이지...ㅎ)

const doubleSelectionSort = (arr) => {
  let start = 0
  let end = arr.length

  while (start < end) {
    let min = start
    let max = end

    for (let i = start; i < end; i++) {
      if (arr[min] > arr[i]) {
        min = i
      }

      if (arr[max] < arr[i]) {
        max = i
      }
    }

    if (start !== min) {
      ;[arr[start], arr[min]] = [arr[min], arr[start]]
    }

    if (end !== max) {
      ;[arr[end], arr[max]] = [arr[max], arr[end]]
    }

    start++
    end--
  }

  return arr
}

마무리

선택정렬 알고리즘은 버블정렬 알고리즘처럼 구현 난이도가 쉬운 편에 속하는 정렬 알고리즘 중 하나입니다. 버블정렬 알고리즘도 구현은 쉬웠으나 실제 사용하는데는 다소 무리가 있는 퍼포먼스를 보인 것 처럼, 선택정렬 알고리즘 또한 실제로 해당 알고리즘을 실무에 적용하기에는 퍼포먼스가 좋지 않고, 비효율적인 면이 있기 때문에 사용하지 않습니다.

하지만 정렬 알고리즘들의 각 원리와 특징을 알아야 효율적인 방향을 찾고, 개선해 나갈 수 있기 때문에 각 정렬 알고리즘들의 특성들을 이해하고 구현할줄 알아야 된다고 생각합니다.

선택정렬 알고리즘의 퍼포먼스가 비효율적인 알고리즘이라고 소개하긴 했지만, 특정 상황에 한정해서 다른 정렬 알고리즘과 비교해서 우위에 있는 방법이 될 수 있습니다. (메모리 사용이 극도로 제한되어 있는 환경이라면 추가적인 메모리가 필요로한 정렬 알고리즘에 비해서 효율적인 알고리즘이라고 볼 수 있겠죠?)

이렇게 각 정렬 알고리즘의 특성을 알고 있어야 상황에 맞춰서 어떻게 구현할지에 대해서 아이디어도 나오는 것이기 때문에 각 알고리즘에 대해 공부하고, 차이점에 대해서 잘 숙지하고 있으면 좋을 것 같습니다.

728x90

그리드형